Monday, April 10, 2017

[Data Structure]Segment Tree



线段树是一种用来解决区间查询和更新的数据结构。对于[m ,n]的区间我们可以把区间递归地二分直到区间的长度变为1。比如储存任意区间和的线段树可以表示为(image from here)：


可以看出，segment tree的每个节点要不有两个子节点要不没有子节点，所以segment tree是一个full binary tree，同时也是一个balance binary tree。对于有n个叶节点的binary tree，有n - 1个非叶节点，所以空间复杂度是O(n), 我们实现的时候用array因为更加方便，但是值得注意的是，开2*n的空间是不够的，因为和heap不同，segment tree不是一个complete binary tree所以其中有一些slot我们是用不上的，一般开3*n差不多够用。这里我们以求区间和为例，建树的时候我们只需bottom up不断用子节点的值更新当前节点即可，时间复杂度O(n)，代码如下，先不用在意mark，我们之后会讲：
struct Node
{
int val;
int mark;
Node() : val(0), mark(0)
{
}
};
SegmentTree(vector<int> nums) {
n = nums.size();
if (!n)return;
st = vector<Node>(3 * n);
createTree(nums, 0, n - 1, 0);
}
void createTree(vector<int>& nums, int lo, int hi, int i)
{
if (lo == hi)
{
st[i].val = nums[lo];
return;
}
int mid = lo + (hi - lo) / 2;
createTree(nums, lo, mid, 2 * i + 1);
createTree(nums, mid + 1, hi, 2 * i + 2);
st[i].val = st[2 * i + 1].val + st[2 * i + 2].val;
}
view raw st_create hosted with ❤ by GitHub


更新的时候我们只需binary search找到要更新的节点然后更新路径上的所有节点，时间复杂度O(log(n))，代码如下：
void update(int start, int end, int add)
{
update(start, end, 0, 0, n - 1, add);
}
void update(int index, int val, int node, int lo, int hi)
{
if (lo == hi)
{
st[node].val = val;
return;
}
int mid = lo + (hi - lo) / 2;
if (index <= mid)update(index, val, 2 * node + 1, lo, mid);
else update(index, val, 2 * node + 2, mid + 1, hi);
st[node].val = st[2 * node + 1].val + st[2 * node + 2].val;
}
view raw st_update hosted with ❤ by GitHub

查询的时候我们要考虑三种情况：

  1. 查询区间和当前区间没有交集，return 0
  2. 查询区间完全包含当前区间，return当前node的值即可
  3. 查询区间和当前区间相交或者当前区间完全包含查询区间，递归地查询两个子区间
那么我们有的时候要查询两个子区间，那么查询的时间复杂度还是O(log(n))吗？设想一下两种情况：
  1. 查询区间没有通过当前区间的中点，那么我们最终只递归查询了一个子区间
  2. 查询区间通过了当前区间的中点，考虑两个子区间c1，c2，我们有以下的结论：
    • 查询区间要不覆盖c1的整个右半边和左半边的一部分，要不只覆盖c1右半边的一部分
    • 查询区间要不覆盖c2的整个左半边和右半边的一部分，要不只覆盖c2左半边的一部分
对于2的情况，如果查询区间覆盖了整个区间的右半部分或者左半部分L，对于L我们只需要只需要直接return当前节点的值即可，不会产生额外的递归，所以对于2的情况，我们每一层最多查询4个节点，两个继续递归的节点，和两个完全覆盖直接return的节点。所以查询的时间复杂度仍然是O(log(n))。代码如下：
int sumRange(int i, int j) {
return sumQuery(i, j, 0, n - 1, 0);
}
int sumQuery(int qlo, int qhi, int clo, int chi, int i)
{
if(qlo > chi || qhi < clo)return 0;
if(qlo <= clo && qhi >= chi)return st[i].val;
int mid = clo + (chi - clo) / 2;
return sumQuery(qlo, qhi, clo, mid, 2 * i + 1) + sumQuery(qlo, qhi, mid + 1, chi, 2 * i + 2);
}
view raw st_query hosted with ❤ by GitHub

对于区间更新，这是segment tree的精华和优势所在，我们采用lazy propagation来把更新的操作分摊到后续的每一次经过该节点的更新和查询上。具体来讲，每个node我们会加一个lazy用来存从父节点得到的更新信息，但是我们不急于apply到当前节点和所有子节点。对于一个完全被包含于更新区间[s, e]的节点node，一般来讲我们需要递归地更新其所有子节点。但是如果应用了lazy propagation，我们只需要更新node对应的值，然后更新两个子节点对应的lazy的值，当下一次我们的某个查询或者更新经过了某个子节点，我们再更具lazy的值更新对应的节点值并且继续传递到子节点。这样的话，我们只有当要用(查询/更新)这个节点的话我们才去更新它，也就是所谓的lazy propagation。此外，我们的更新信息也不会丢失因为每当applylazy的信息的时候我们都会传递给子节点知道叶节点。区间更新的时间复杂度也是O(log(n))，分析和查询类似，查询的时候我们只多了每一个节点向子节点传播mark的时间，所以仍然是O(log(n))。代码如下：
void update(int start, int end, int add)
{
update(start, end, 0, 0, n - 1, add);
}
void update(int s, int e, int node, int lo, int hi, int add)
{
if (st[node].mark)propagate(node, hi - lo + 1);
if (lo > e || hi < s)return;
if (s <= lo && e >= hi)
{
st[node].val += add;
if (lo != hi)
{
st[2 * node + 1].mark += add;
st[2 * node + 2].mark += add;
}
return;
}
int mid = lo + (hi - lo) / 2;
update(s, e, 2 * node + 1, lo, mid, add);
update(s, e, 2 * node + 2, mid + 1, hi, add);
st[node].val = st[2 * node + 1].val + st[2 * node + 2].val;
}
void propagate(int node, int len)
{
st[node].val += len * st[node].mark;
if (len != 1)
{
st[2 * node + 1].mark += st[node].mark;
st[2 * node + 2].mark += st[node].mark;
}
st[node].mark = 0;
}
int sumQuery(int qlo, int qhi, int clo, int chi, int i)
{
if(st[i].mark)propagate(i, chi - clo + 1);
if (qlo > chi || qhi < clo)return 0;
if (qlo <= clo && qhi >= chi)return st[i].val;
int mid = clo + (chi - clo) / 2;
int res = sumQuery(qlo, qhi, clo, mid, 2 * i + 1) + sumQuery(qlo, qhi, mid + 1, chi, 2 * i + 2);
}
view raw st_range_update.cxx hosted with ❤ by GitHub

完整代码如下：
struct Node
{
int val;
int mark;
Node() : val(0), mark(0)
{
}
};
class NumArray {
public:
NumArray(vector<int> nums) {
n = nums.size();
if (!n)return;
st = vector<Node>(3 * n);
createTree(nums, 0, n - 1, 0);
}
void update(int i, int val) {
update(i, val, 0, 0, n - 1);
}
void update(int start, int end, int add)
{
update(start, end, 0, 0, n - 1, add);
}
int sumRange(int i, int j) {
return sumQuery(i, j, 0, n - 1, 0);
}
private:
int n;
vector<Node> st;
void createTree(vector<int>& nums, int lo, int hi, int i)
{
if (lo == hi)
{
st[i].val = nums[lo];
return;
}
int mid = lo + (hi - lo) / 2;
createTree(nums, lo, mid, 2 * i + 1);
createTree(nums, mid + 1, hi, 2 * i + 2);
st[i].val = st[2 * i + 1].val + st[2 * i + 2].val;
}
void update(int index, int val, int node, int lo, int hi)
{
if (lo == hi)
{
st[node].val = val;
return;
}
int mid = lo + (hi - lo) / 2;
if (index <= mid)update(index, val, 2 * node + 1, lo, mid);
else update(index, val, 2 * node + 2, mid + 1, hi);
st[node].val = st[2 * node + 1].val + st[2 * node + 2].val;
}
void update(int s, int e, int node, int lo, int hi, int add)
{
if (st[node].mark)propagate(node, hi - lo + 1);
if (lo > e || hi < s)return;
if (s <= lo && e >= hi)
{
st[node].val += add;
if (lo != hi)
{
st[2 * node + 1].mark += add;
st[2 * node + 2].mark += add;
}
return;
}
int mid = lo + (hi - lo) / 2;
update(s, e, 2 * node + 1, lo, mid, add);
update(s, e, 2 * node + 2, mid + 1, hi, add);
st[node].val = st[2 * node + 1].val + st[2 * node + 2].val;
}
void propagate(int node, int len)
{
st[node].val += len * st[node].mark;
if (len != 1)
{
st[2 * node + 1].mark += st[node].mark;
st[2 * node + 2].mark += st[node].mark;
}
st[node].mark = 0;
}
int sumQuery(int qlo, int qhi, int clo, int chi, int i)
{
if(st[i].mark)propagate(i, chi - clo + 1);
if (qlo > chi || qhi < clo)return 0;
if (qlo <= clo && qhi >= chi)return st[i].val;
int mid = clo + (chi - clo) / 2;
int res = sumQuery(qlo, qhi, clo, mid, 2 * i + 1) + sumQuery(qlo, qhi, mid + 1, chi, 2 * i + 2);
return res;
}
};
view raw segment_tree.cxx hosted with ❤ by GitHub





2D扩展

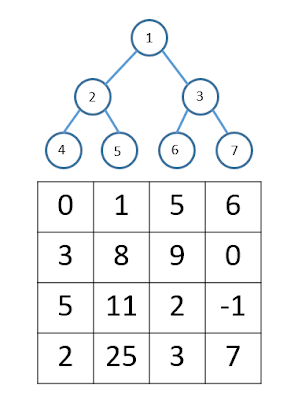
2D Segment Tree可以用来查询2D的range query。值得注意的是，2D Segment Tree并不是QuadTree。2D Segment Tree的每一个节点都是一个1D的Segment Tree，我们以Region Sum为例：


对应的4,5,6,7节点分别对应矩阵第1,2,3,4列的1D Segment Tree。2,3节点分别对应1,2列的和与3,4列的和形成的1D Segment Tree，1号节点就为所有列的和所形成的segment tree。2D的construct，query和update和1D是十分类似的。假设输入矩阵为O(m * n)，以上操作对应时间复杂度分别为O(m * n), O(log(m) * log(n)) 和O(log(m) * log(n))。空间复杂度O(m * n)，代码如下：


class SegmentTree
{
public:
SegmentTree(vector<int>& nums)
{
n = nums.size();
m_st = vector<int>(3 * n, 0);
createTree(0, n - 1, 0, nums);
}
void update(int i, int add)
{
updateTree(0, n - 1, i, 0, add);
}
int query(int lo, int hi)
{
return query(lo, hi, 0, n - 1, 0);
}
private:
vector<int> m_st;
int n;
void createTree(int lo, int hi, int i, vector<int>& nums)
{
if(lo == hi)
{
m_st[i] = nums[lo];
return;
}
int mid = lo + (hi - lo) / 2;
createTree(lo, mid, 2 * i + 1, nums);
createTree(mid + 1, hi, 2 * i + 2, nums);
m_st[i] = m_st[2 * i + 1] + m_st[2 * i + 2];
}
void updateTree(int lo, int hi, int idx, int i, int add)
{
if(lo == hi)
{
m_st[i] += add;
return;
}
int mid = lo + (hi - lo) / 2;
if(idx <= mid)
updateTree(lo, mid, idx, 2 * i + 1, add);
else
updateTree(mid + 1, hi, idx, 2 * i + 2, add);
m_st[i] = m_st[2 * i + 1] + m_st[2 * i + 2];
}
int query(int qlo, int qhi, int lo, int hi, int i)
{
int mid = lo + (hi - lo) / 2;
if(qlo > hi || qhi < lo)
return 0;
else if(qlo <= lo && qhi >= hi)
return m_st[i];
else
return query(qlo, qhi, lo, mid, 2 * i + 1) + query(qlo, qhi, mid + 1, hi, 2 * i + 2);
}
};
class NumMatrix {
public:
NumMatrix(vector<vector<int>> matrix) {
nums = matrix;
m = matrix.size();
int n = m? matrix[0].size(): 0;
if(!m || !n)return;
m_st = vector<SegmentTree*>(3 * m, nullptr);
createTree(0, m - 1, 0, matrix);
}
~NumMatrix()
{
for(auto ptr : m_st)
{
if(ptr)
delete ptr;
}
}
void update(int row, int col, int val) {
int diff = val - nums[row][col];
update(0, m - 1, row, col, 0, diff);
nums[row][col] = val;
}
int sumRegion(int row1, int col1, int row2, int col2) {
return query(row1, row2, col1, col2, 0, m - 1, 0);
}
private:
vector<SegmentTree*> m_st;
vector<vector<int>> nums;
int m;
vector<int> createTree(int lo, int hi, int i, vector<vector<int>>& matrix)
{
if(lo == hi)
{
m_st[i] = new SegmentTree(matrix[lo]);
return matrix[lo];
}
int mid = lo + (hi - lo) / 2;
auto v1 = createTree(lo, mid, 2 * i + 1, matrix);
auto v2 = createTree(mid + 1, hi, 2 * i + 2, matrix);
for(int i = 0; i < v1.size(); ++i)
v1[i] += v2[i];
m_st[i] = new SegmentTree(v1);
return v1;
}
void update(int lo, int hi, int i, int j, int idx, int add)
{
if(lo == hi)
{
m_st[idx]->update(j, add);
return;
}
int mid = lo + (hi - lo) / 2;
if(i <= mid)
update(lo, mid, i, j, 2 * idx + 1, add);
else
update(mid + 1, hi, i, j, 2 * idx + 2, add);
m_st[idx]->update(j, add);
}
int query(int xlo, int xhi, int ylo, int yhi, int lo, int hi, int i)
{
int mid = lo + (hi - lo) / 2;
if(xhi < lo || xlo > hi)
return 0;
else if(xlo <= lo && xhi >= hi)
return m_st[i]->query(ylo, yhi);
else
return query(xlo, xhi, ylo, yhi, lo, mid, 2 * i + 1) + query(xlo, xhi, ylo, yhi, mid + 1, hi, 2 * i + 2);
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* obj.update(row,col,val);
* int param_2 = obj.sumRegion(row1,col1,row2,col2);
*/
view raw Range Sum Query 2D - Mutable_I.cpp hosted with ❤ by GitHub


Posted by at
Labels: ,
Location: Redwood City, CA, USA

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)