[POJ]3040 Fibonacci

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_{n − 1} + F_{n − 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

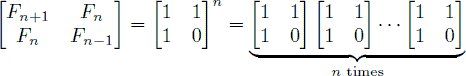Given an integer n, your goal is to compute the last 4 digits of F_n.

题目已经告诉我们了求[[1, 1], [1, 0]]的n次方可以求得斐波那契的第n项，那么我们用快速幂就可以在O(log n)的时间内求得答案，快速幂的文章可以参考这篇。代码如下：