[Algorithm]KMP Algorithm

KMP算法第一眼看上去可能会让人懵逼，但是其实仔细搞懂之后还是比较好理解的，核心代码并不复杂并且可以被应用到很多题上。这一篇文章会大概介绍KMP的思路和如何计算next数组，如果需要更详细的讲解，可以参考这篇文章。
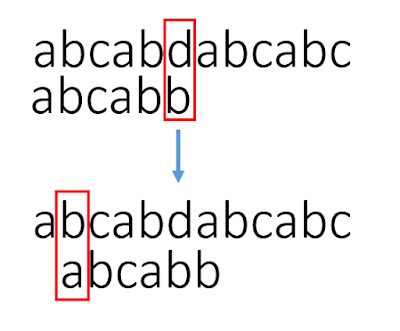
假设我们有两个string s和t，我们要寻找t是否在s当中出现。普通的字符匹配算法是，假设s匹配到i，t匹配到j，我们check s[i]和t[j]是否相等。如果相等的话我们继续匹配下一位，否则i会回溯到这一轮匹配的起点的下一位，如下所示：

换句话说，i是有可能往回走的。很显然这效率不高，假设s长n，t长m，最坏情况时间复杂度可能达到O(m * n)。并且我们可以看到其实在匹配到最后一位的时候，前面已经匹配的所有位已经给了我们一些信息，可以让我们不回溯i，只移动j，如下图所示：

我们可以看到，因为t中c之前的ab我们在上一轮匹配的时候已经匹配过了，并且我们知道t是以ab开头的，那么我们完全可以跳过s中间的所有字符，直接把j移动到c继续匹配即可。这就是KMP算法可以让我们做到的，KMP算法中i永远不会回溯，并且时间复杂度是O(n + m) ，这个我们之后会详细分析。
KMP如何可以做到这一点呢，我们先看代码：



我们可以看到，当每一次失配的时候，j是移动到next[j]的。那么next数组是什么？我们又应该如何求呢？为了便于理解，我们先考虑，对于一个string t，如何求其最长的公共前后缀p，并且p不能为t自身，如下图所示：

以string t，abcdabd为例，假设我们用LCPS[i](Longest common prefix and suffix)来表示前i个数的LCPS，我们可以得到以下数组：

第一个a虽然LCPS为0，但是为了便于得知其为string的起始位置，我们给它标记为-1。那么这个数组用处是什么呢。假设t匹配到t[6] == d的时候发现其和s对应的位置i并不适配。这时候我们发现t的前六个字符也就是d前面的所有字符，其有一个长度为2的最长公共前后缀。这代表了abcdab中后缀ab已经和s中某两位匹配过了，那么前缀ab可以直接移动到后缀ab的位置然后让c继续和s中的i位进行匹配。也就是我们一开始的图中所示的i不回溯的方法。
那么我们在s中跳过了一些字符，直接放弃以其为起始点再度匹配，为什么我们可以确定不用去再次匹配呢？那么在上面的例子中，s中已经匹配过的字符就是abcdab，也就是t中的前六个字符，我们知道其LCPS的长度为2，这代表什么呢？这代表前缀ab的下一次匹配的起始位置只能从后缀ab开始，因为其他更长的后缀都没有对应的公共前缀，比如dab，cdab，bcdab，这些在s中都对应以i - 3, i -4, i - 5位置开头的substring。我们完全可以把以ab开头的string t跳过这些位置，因为我们可以断定string t不会和s中以这些位置开头的substring匹配。
所以我们知道next数组为何可以正确的指示j下一次的匹配位置，那么我们如何求next数组呢。
求next数组的代码如下，就是之前贴过的代码的一部分：



i代表当前匹配的后缀尾端，k代表当前匹配的前缀尾端。第5行是比较好理解的，如果当前i和k适配，我们各自移动到下一位并且更新next数组当前LCPS的长度，也就是++k的长度。但是如何理解第7行，也就是当k和i的位置不适配是，k要移动到next[k]。这个是求next数组中最核心的部分，我们以abacabab作为例子：

当k扫到c，i扫到b的时候，我们发现前缀后缀不不匹配了，我们之前匹配到的LCPS是aba，然而aba无法让k和j匹配，那么我们应该寻找abacaba中比aba短的最长的公共前后缀继续匹配，也就是将k移动到比aba短的最长的公共前后缀的下一位继续试图和i位匹配，因为只有这样才能保证我们找到的公共前后缀永远是最长的。那么比aba短的最长的公共前后缀如何寻找呢，首先我们肯定它一定比aba短，也就是说它一定是aba的某个前缀，那么满足条件的不正是aba的LCPS么。因为首先aba为abacaba的公共前后缀，所以aba的公共前后缀，也是当前abacaba的公共前后缀。并且aba的LCPS，也就是abacaba的比LCPS短的最长的公共前后缀。对于这个例子，k=next[k]，的结果也就是使k移动到下一个公共前后缀之后，也就是b的位置。因为这个例子当中，比aba短的最长的公共前后缀就是a了。我们可以继续匹配k位的b和j位的b。
理解了以上的方法，我们就可以在O(m)的时间求出next数组，然后按照next数组的指示，在s和t失配的时候移动j的位置。我们可以观察出i永远不会回溯，但是我们的j是有可能回溯的，那么匹配的时间复杂度还是O(n)么?
要分析这一点，我们首先看j可能增加多少次，因为j的增加和i的增加是同步的，所以j最多增加n次，也就是s的长度。那么j = next[j]是减小j的操作，并且j最小值为-1，很显然我们减小j的操作也是不可能超过n的，不然的话j就小于-1了。所以平摊下来总的时间复杂度还是O(n)。之前我们求next数组的时候k也会回溯，我们用同样的方法分析可得求next数组的时间复杂度为O(m)，所以总的时间复杂度为O(m + n)。


KMP的优化，对于如下的例子：

我们可以看出来在d和c失配之后，根据我们的next数组我们又让d和c去匹配了。这个问题出现的原因是，因为我们在构建next数组的时候，发现t[k] == t[i]的时候，直接就让next[i + 1] = k + 1，事实上我们们应该先check一下i + 1和k +1位的字符是否相同因为如果相同的话，到时候j = next[j]之后还要匹配的仍然是一样的字符。所以如果相同的话，我们让next[i + 1] = next[k + 1]，如下图所示：

所以我们可以进一步优化KMP的代码，代码如下：