[POJ]1548 Robots

Your company provides robots that can be used to pick up litter from fields after sporting events and concerts. Before robots are assigned to a job, an aerial photograph of the field is marked with a grid. Each location in the grid that contains garbage is marked. All robots begin in the Northwest corner and end their movement in the Southeast corner. A robot can only move in two directions, either to the East or South. Upon entering a cell that contains garbage, the robot will pick it up before proceeding. Once a robot reaches its destination at the Southeast corner it cannot be repositioned or reused. Since your expenses are directly proportional to the number of robots used for a particular job, you are interested in finding the minimum number of robots that can clean a given field. For example, consider the field map shown in Figure 1 with rows and columns numbered as shown and garbage locations marked with a 'G'. In this scheme, all robots will begin in location 1,1 and end in location 6, 7. 

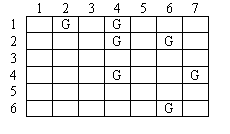
Figure 1 - A Field Map
Figure 2 below shows two possible solutions, the second of which is preferable since it uses two robots rather than three. 

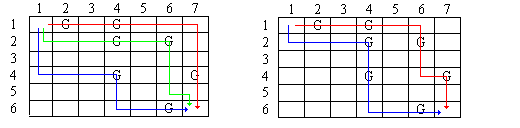
Figure 2 - Two Possible Solutions
Your task is to create a program that will determine the minimum number of robots needed to pick up all the garbage from a field. 


如果我们根据所有的垃圾所在的点建图：

• 对于节点(x, y)和(i, j)，如果x <= i && y <= j，那么会有(x, y)连向(i, j)的一条有向边

这个图肯定无环，所以必定是DAG。所以这道题就变成了，在DAG中寻找最少的路径，从而可以覆盖所有的节点，每一个节点只对应一条路径。这就是DAG的最小路径覆盖问题，根据这篇文章，DAG的最小路径覆盖可以转化成二分图的最大匹配问题。所以我们建对应的二分图然后跑匈牙利算法即可，时间复杂度O(V * E)，代码如下：