[POJ]2446 ChessBoard

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below). 

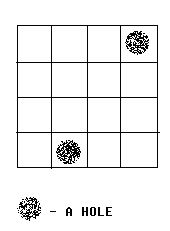
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below: 
1. Any normal grid should be covered with exactly one card. 
2. One card should cover exactly 2 normal adjacent grids. 

Some examples are given in the figures below: 

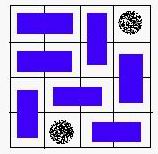
A VALID solution.

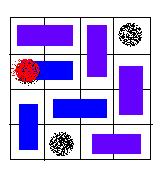
An invalid solution, because the hole of red color is covered with a card.

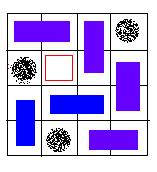
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

如果我们把每个棋盘的格子看做顶点，相邻的格子有边相连的话，那么棋盘就可以表示成一个二分图，因为只有黑色的格子和白色的格子之间才有边连接。黑色和黑色，白色和白色之间都没有边相连。那么这道题就相当于建图之后求最大匹配是否能覆盖图中的所有节点，求最大匹配的算法参考这篇文章。时间复杂度O(V*E)，代码如下：